linear drawing of a tree

What is a Tree data structure?

A tree is non-linear and a hierarchical data structure consisting of a collection of nodes such that each node of the tree stores a value and a list of references to other nodes (the "children").

This data structure is a specialized method to organize and store data in the computer to be used more effectively. It consists of a central node, structural nodes, and sub-nodes, which are connected via edges. We can also say that tree data structure has roots, branches, and leaves connected with one another.

Recursive Definition:

A tree consists of a root, and zero or more subtrees T₁, T₂, … , T_k such that there is an edge from the root of the tree to the root of each subtree.

Why Tree is considered a non-linear data structure?

The data in a tree are not stored in a sequential manner i.e, they are not stored linearly. Instead, they are arranged on multiple levels or we can say it is a hierarchical structure. For this reason, the tree is considered to be a non-linear data structure.

Basic Terminologies In Tree Data Structure:

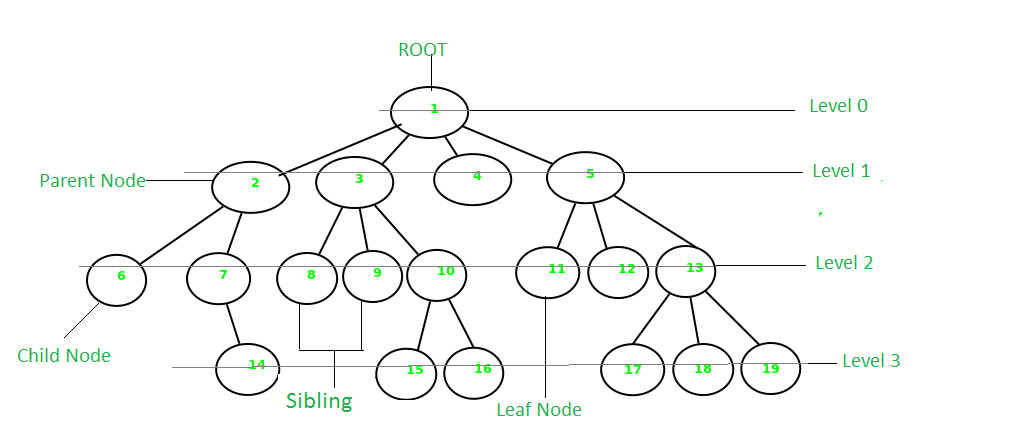
• Parent Node: The node which is a predecessor of a node is called the parent node of that node. {2} is the parent node of {6, 7}.
• Child Node: The node which is the immediate successor of a node is called the child node of that node. Examples: {6, 7} are the child nodes of {2}.
• Root Node: The topmost node of a tree or the node which does not have any parent node is called the root node. {1} is the root node of the tree. A non-empty tree must contain exactly one root node and exactly one path from the root to all other nodes of the tree.
• Leaf Node or External Node: The nodes which do not have any child nodes are called leaf nodes. {6, 14, 8, 9, 15, 16, 4, 11, 12, 17, 18, 19} are the leaf nodes of the tree.
• Ancestor of a Node: Any predecessor nodes on the path of the root to that node are called Ancestors of that node. {1, 2} are the ancestor nodes of the node {7}
• Descendant: Any successor node on the path from the leaf node to that node. {7, 14} are the descendants of the node. {2}.
• Sibling: Children of the same parent node are called siblings. {8, 9, 10} are called siblings.
• Level of a node: The count of edges on the path from the root node to that node. The root node has level 0.
• Internal node: A node with at least one child is called Internal Node.
• Neighbour of a Node: Parent or child nodes of that node are called neighbors of that node.
• Subtree: Any node of the tree along with its descendant.

Properties of a Tree:

• Number of edges: An edge can be defined as the connection between two nodes. If a tree has N nodes then it will have (N-1) edges. There is only one path from each node to any other node of the tree.
• Depth of a node: The depth of a node is defined as the length of the path from the root to that node. Each edge adds 1 unit of length to the path. So, it can also be defined as the number of edges in the path from the root of the tree to the node.
• Height of a node: The height of a node can be defined as the length of the longest path from the node to a leaf node of the tree.
• Height of the Tree: The height of a tree is the length of the longest path from the root of the tree to a leaf node of the tree.
• Degree of a Node: The total count of subtrees attached to that node is called the degree of the node. The degree of a leaf node must be 0. The degree of a tree is the maximum degree of a node among all the nodes in the tree.

Some more properties are:

• Traversing in a tree is done by depth first search and breadth first search algorithm.
• It has no loop and no circuit
• It has no self-loop
• Its hierarchical model.

Syntax:

struct Node
{
   int data;
   struct Node *left_child;
   struct Node *right_child;
};

Basic Operation Of Tree:

Create – create a tree in data structure.
Insert − Inserts data in a tree.
Search − Searches specific data  in a tree to check it is present or not.
Preorder Traversal – perform Traveling a tree in a pre-order manner in data structure .
In order Traversal – perform Traveling a tree in an in-order manner.
Post order Traversal –perform Traveling a tree in a post-order manner.

Example of Tree data structure

Here,

Node A is the root node

B is the parent of D and E

D and E are the siblings

D, E, F and G are the leaf nodes

A and B are the ancestors of E

Few examples on Tree Data Structure: A code to demonstrate few of the above terminologies has been described below:

C++

#include <bits/stdc++.h>

using namespace std;

void addEdge( int x, int y, vector<vector< int > >& adj)

{

adj[x].push_back(y);

adj[y].push_back(x);

}

void printParents( int node, vector<vector< int > >& adj,

int parent)

{

if (parent == 0)

cout << node << "->Root" << endl;

else

cout << node << "->" << parent << endl;

for ( auto cur : adj[node])

if (cur != parent)

printParents(cur, adj, node);

}

void printChildren( int Root, vector<vector< int > >& adj)

{

queue< int > q;

q.push(Root);

int vis[adj.size()] = { 0 };

while (!q.empty()) {

int node = q.front();

q.pop();

vis[node] = 1;

cout << node << "-> " ;

for ( auto cur : adj[node])

if (vis[cur] == 0) {

cout << cur << " " ;

q.push(cur);

}

cout << endl;

}

}

void printLeafNodes( int Root, vector<vector< int > >& adj)

{

for ( int i = 1; i < adj.size(); i++)

if (adj[i].size() == 1 && i != Root)

cout << i << " " ;

cout << endl;

}

void printDegrees( int Root, vector<vector< int > >& adj)

{

for ( int i = 1; i < adj.size(); i++) {

cout << i << ": " ;

if (i == Root)

cout << adj[i].size() << endl;

else

cout << adj[i].size() - 1 << endl;

}

}

int main()

{

int N = 7, Root = 1;

vector<vector< int > > adj(N + 1, vector< int >());

addEdge(1, 2, adj);

addEdge(1, 3, adj);

addEdge(1, 4, adj);

addEdge(2, 5, adj);

addEdge(2, 6, adj);

addEdge(4, 7, adj);

cout << "The parents of each node are:" << endl;

printParents(Root, adj, 0);

cout << "The children of each node are:" << endl;

printChildren(Root, adj);

cout << "The leaf nodes of the tree are:" << endl;

printLeafNodes(Root, adj);

cout << "The degrees of each node are:" << endl;

printDegrees(Root, adj);

return 0;

}

Java

import java.io.*;

import java.util.*;

class GFG {

public static void

printParents( int node, Vector<Vector<Integer> > adj,

int parent)

{

if (parent == 0 )

System.out.println(node + "->Root" );

else

System.out.println(node + "->" + parent);

for ( int i = 0 ; i < adj.get(node).size(); i++)

if (adj.get(node).get(i) != parent)

printParents(adj.get(node).get(i), adj,

node);

}

public static void

printChildren( int Root, Vector<Vector<Integer> > adj)

{

Queue<Integer> q = new LinkedList<>();

q.add(Root);

int vis[] = new int [adj.size()];

Arrays.fill(vis, 0 );

while (q.size() != 0 ) {

int node = q.peek();

q.remove();

vis[node] = 1 ;

System.out.print(node + "-> " );

for ( int i = 0 ; i < adj.get(node).size(); i++) {

if (vis[adj.get(node).get(i)] == 0 ) {

System.out.print(adj.get(node).get(i)

+ " " );

q.add(adj.get(node).get(i));

}

}

System.out.println();

}

}

public static void

printLeafNodes( int Root, Vector<Vector<Integer> > adj)

{

for ( int i = 1 ; i < adj.size(); i++)

if (adj.get(i).size() == 1 && i != Root)

System.out.print(i + " " );

System.out.println();

}

public static void

printDegrees( int Root, Vector<Vector<Integer> > adj)

{

for ( int i = 1 ; i < adj.size(); i++) {

System.out.print(i + ": " );

if (i == Root)

System.out.println(adj.get(i).size());

else

System.out.println(adj.get(i).size() - 1 );

}

}

public static void main(String[] args)

{

int N = 7 , Root = 1 ;

Vector<Vector<Integer> > adj

= new Vector<Vector<Integer> >();

for ( int i = 0 ; i < N + 1 ; i++) {

adj.add( new Vector<Integer>());

}

adj.get( 1 ).add( 2 );

adj.get( 2 ).add( 1 );

adj.get( 1 ).add( 3 );

adj.get( 3 ).add( 1 );

adj.get( 1 ).add( 4 );

adj.get( 4 ).add( 1 );

adj.get( 2 ).add( 5 );

adj.get( 5 ).add( 2 );

adj.get( 2 ).add( 6 );

adj.get( 6 ).add( 2 );

adj.get( 4 ).add( 7 );

adj.get( 7 ).add( 4 );

System.out.println( "The parents of each node are:" );

printParents(Root, adj, 0 );

System.out.println(

"The children of each node are:" );

printChildren(Root, adj);

System.out.println(

"The leaf nodes of the tree are:" );

printLeafNodes(Root, adj);

System.out.println( "The degrees of each node are:" );

printDegrees(Root, adj);

}

}

Python3

def printParents(node, adj, parent):

if (parent = = 0 ):

print (node, "->Root" )

else :

print (node, "->" , parent)

for cur in adj[node]:

if (cur ! = parent):

printParents(cur, adj, node)

def printChildren(Root, adj):

q = []

q.append(Root)

vis = [ 0 ] * len (adj)

while ( len (q) > 0 ):

node = q[ 0 ]

q.pop( 0 )

vis[node] = 1

print (node, "-> " , end = " " )

for cur in adj[node]:

if (vis[cur] = = 0 ):

print (cur, " " , end = " " )

q.append(cur)

print ( "\n" )

def printLeafNodes(Root, adj):

for i in range ( 0 , len (adj)):

if ( len (adj[i]) = = 1 and i ! = Root):

print (i, end = " " )

print ( "\n" )

def printDegrees(Root, adj):

for i in range ( 1 , len (adj)):

print (i, ": " , end = " " )

if (i = = Root):

print ( len (adj[i]))

else :

print ( len (adj[i]) - 1 )

N = 7

Root = 1

adj = []

for i in range ( 0 , N + 1 ):

adj.append([])

adj[ 1 ].append( 2 )

adj[ 2 ].append( 1 )

adj[ 1 ].append( 3 )

adj[ 3 ].append( 1 )

adj[ 1 ].append( 4 )

adj[ 4 ].append( 1 )

adj[ 2 ].append( 5 )

adj[ 5 ].append( 2 )

adj[ 2 ].append( 6 )

adj[ 6 ].append( 2 )

adj[ 4 ].append( 7 )

adj[ 7 ].append( 4 )

print ( "The parents of each node are:" )

printParents(Root, adj, 0 )

print ( "The children of each node are:" )

printChildren(Root, adj)

print ( "The leaf nodes of the tree are:" )

printLeafNodes(Root, adj)

print ( "The degrees of each node are:" )

printDegrees(Root, adj)

Output

The parents of each node are: 1->Root 2->1 5->2 6->2 3->1 4->1 7->4 The children of each node are: 1-> 2 3 4  2-> 5 6  3->  4-> 7  5->  6->  7->  The leaf nodes of the tree are: 3 5 6 7  The degrees of each node are: 1: 3 2: 2 3: 0 4: 1 5: 0 6: 0 7: 0

Types of Tree data structures

The different types of tree data structures are as follows:

1. General tree

A general tree data structure has no restriction on the number of nodes. It means that a parent node can have any number of child nodes.

2. Binary tree

A node of a binary tree can have a maximum of two child nodes. In the given tree diagram, node B, D, and F are left children, while E, C, and G are the right children.

3. Balanced tree

If the height of the left sub-tree and the right sub-tree is equal or differs at most by 1, the tree is known as a balanced tree.

   Balanced Tree                                                                      Unbalanced Tree

4. Binary search tree

As the name implies, binary search trees are used for various searching and sorting algorithms. The examples include AVL tree and red-black tree. It is a non-linear data structure. It shows that the value of the left node is less than its parent, while the value of the right node is greater than its parent.

Applications of Tree data structure:

The applications of tree data structures are as follows:

1. Spanning trees: It is the shortest path tree used in the routers to direct the packets to the destination.

2. Binary Search Tree: It is a type of tree data structure that helps in maintaining a sorted stream of data.

1. Full Binary tree
2. Complete Binary tree
3. Skewed Binary tree
4. Strictly Binary tree
5. Extended Binary tree

3. Storing hierarchical data: Tree data structures are used to store the hierarchical data, which means data is arranged in the form of order.

4. Syntax tree: The syntax tree represents the structure of the program's source code, which is used in compilers.

5. Trie: It is a fast and efficient way for dynamic spell checking. It is also used for locating specific keys from within a set.

6. Heap: It is also a tree data structure that can be represented in a form of an array. It is used to implement priority queues.

lewisupong1989.blogspot.com

Source: https://www.geeksforgeeks.org/introduction-to-tree-data-structure-and-algorithm-tutorials/

Share this post